[혼공분석] with 파이썬 4주차 공부 ( 4주차 추가 숙제 포함)
4-1 통계로 요약하기
(1) 기술통계(=요약통계) 용어 정리
- 기술통계: 자료의 내용을 압축하여 설명하는 방법
- 통계량 : 평균, 표준편차 등
- 탐색적 데이터 분석 : 데이터 시각화를 아우르는 데이터 분석 방법
(2) 기술통계 구하기 ( 4주차 추가 과제 포함)
1) describe() 메소드 : 수치 타입 열의 기술통계를 자동으로 추출함.
(% 지정하는 매개변수 : percentiles = [0.3, 0.6, 0.9]
예시.

- count : (누락된 값을 제외)데이터 개수
- mean : 평균
- std : 표준편차
- min, max : 최소, 최대
- 50% : 중앙값
- 25% , 75% : 순서대로 늘어놓았을때 25% 위치한 값, 75% 위치한 값.
2) include() : 수치 외에 다른 데이터 타입 열의 기술통계 확인하기
예시.

- count : (누락된 값 제외) 데이터 수
- unique : 고유한 값 개수
- top : 가장 많이 등장한 값
- freq : top행에 등장하는 항목의 빈도수
( 예. 승정원일기 항목은 도서명 열에서 가장 많은 빈도로 등장하며, 그 수는 250 이다.)
3) 평균, 중앙값, 구하기
- 판다스 데이터 프레임, 시리즈에서 제공하는 기술통계 함수 : mean(), median() , min(), max() ,
- 중앙값을 구하는 메소드 median()은 데이터 개수가 짝수인 경우 가운데 두 개의 값의 평균을 중앙값으로 반환함.
- 목표 : 중복값 제거하고 중앙값 구하기 -> 중복값 제거 함수인 drop_duplicates() -> median()
-quantile : 분위수 구하는 함수
- 분위수 : 데이터를 순서대로 늘어놓았을 때 이를 균등한 간격으로 나누는 기준점
4) 백분위 구하기
: 분위수와는 반대로 특정 값이 어느 위치에 있는지 찾는 방식이 백분위.
예시. 남산도서관 대출 데이터에서 대출건수 10이 위치한 백분위 찾기.
먼저 대출건수열에서 10 미만인 행을 True로 출력해서 시리즈 구성하기
->이제 평균을 구하면
-> 전체에 대한 10 미만의 데이터 비율을 구할 수 있음.
print('대출건수 10의 백분위 :', (ns_book7['대출건수'] < 10).mean(), '(대략 65%)')
# mean()메소드는 판다스 시리즈에도 적용 가능.
print('65% 분위수: ', ns_book7['대출건수'].quantile(0.65))
5) 분산 구하기 : var() 메소드
- 매개변수 ddof
6) 표준편차 구하기 : std() 혹은 np.std()
- 적용 예시.
#방법1. std() 바로 적용
ns_book7['대출건수'].std()
# 방법2. np.std()에 대입
import numpy as np
np.std(ns_book7['대출건수'])
7) 최빈값 구하기 : 열 고르고 -> mode() 메소드
예시. 가장 많은 빈도수로 등장하는 도서명 찾고, 해당 열부터 마지막 열까지 범위에서 출력.
-> 열 범위 지정 -> 최빈값 찾기

4-2 분포 요약하기
1. 산점도 그리기 -> scatter 함수를 이용하기
(1) 예시. 남산도서관 대출 데이터를 이용한 산점도 그리기 ( x축 : 번호 열, y축 : 대출건수 열)
plt.scatter(ns_book7['번호'],ns_book7['대출건수'])
plt.show()
출력 결과

1) 투명도 조절하기 -> 매개변수 alpha
- alpha의 값은 0~1 사이의 값을 가지며, 1에 가까울수록 불투명해진다.
#투명도 조절하기
plt.scatter(ns_book7['도서권수'],ns_book7['대출건수'],alpha = 0.1) # 0~1, 1에 가까울 수록 불투명해짐
plt.show()
출력결과

2) 변수간 관계
- x에 따라 y의 값도 증가 -> 정비례-> 양의 상관관계
- x에 따라 y의 값은 감소 -> 반비례 -> 음의 상관관계
예시. 대출건수와 도서권수 열의 관계 알아보기
#대출건수와 도서권수 열의 관계 알아보기
average_borrows = ns_book7['대출건수']/ns_book7['도서권수'] #전체 도서권수 대비 대출권수
plt.scatter(average_borrows, ns_book7['대출건수'], alpha = 0.1)
plt.show()
출력 결과 : 양의 상관관계를 확인할 수 있다.

2. 히스토그램 그리기
(1) 용어 설명
(2) 히스토그램 그리기 -> hist( ) 함수
예시.
plt.hist([0,3,5,6,7,7,9,13], bins = 5) # bins 매개변수는 구간의 개수
plt.show()
출력 결과

(3) 히스토그램 구간의 확인 -> 넘파이에서 제공하는 histogram_bin_edges( [값 리스트], bins = 개수) 함수
(4) 구간 조정하기
- 한 구간의 도수가 너무 커서 다른 구간에 도수가 표시되지 않는다면
-> y축을 로그 스케일로 바꾸면 된다.
-> plt.yscale('log')
- 로그함수를 이용하면 기존에 간격 10배 차이를 2배 차이로 만들어 더 확장된 그래프를 보여준다.
- 적용예시 1. 대출건수 열에 로그함수를 적용해보자.
# 로그함수 적용 전
plt.hist(ns_book7['대출건수'], bins=100)
plt.show()
# 로그함수 적용 후
plt.hist(ns_book7['대출건수'])
plt.yscale('log')
plt.show()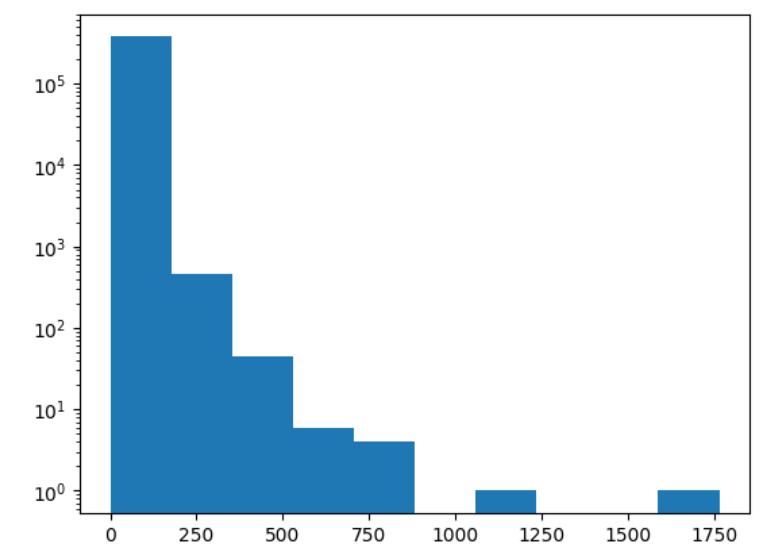
- 적용예시2. 도서명 길이를 히스토그램으로 표현하고 조정해보자.
#조정 전
title_len = ns_book7['도서명'].apply(len)
plt.hist(title_len,bins = 100)
plt.show()
title_len.mean(),title_len.std()
#조정 후
plt.hist(title_len, bins = 100)
plt.xscale('log')
plt.show()

(5) 히스토그램은 하나의 특성에 대한 분포를 확인하는 데 유용.
-> 하지만 여러 특성을 비교하려면 각기 따로 그린 히스토그램을 비교해야 한다.
-> 축의 범위도 잘 맞추어야 한다.
-> 그렇다면 여러 특성을 편리하게 비교하는 방법은 없을까?
3. 상자 수염 그림 그리기
(1) 상자 수염 그림의 구성
- 최솟값, 최대값
- 세 개의 사분위수
(2) 상자 수염 그리는 방법
1) 25%, 75% 사분위 수를 밑면과 윗면으로 하는 직사각형 그리기 (직사각형 높이 = IQR)
2) 50% 해당 지점에 수평선 긋기
3) 직사각형의 높이의 1.5배만큼 떨어진 거리 안에서 가장 멀리 있는 샘플까지 수직선을 긋는다.(=수염 길이)
4) 이 수치선 밖에서 최솟값과 최댓값까지 데이터를 점으로 표시한다. (= 이상치)
(3) 상자수염 그림 -> boxplot( ) 함수
1) 예시. 대출건수와 도서권수로 박스 수염 그림 그리기
# 직사각형이 거의 보이지 않기 때문에 더 넓혀서 보기 위해 로그 스케일을 사용하여 조정한다.
plt.boxplot(ns_book7[['대출건수','도서권수']])
plt.yscale('log')
plt.show()
2) 상자 수염 그림을 수평으로 그리기
-> 매개변수 vert = False 로 하기
# 상자 수염 그림을 수평으로 그리기
plt.boxplot(ns_book7[['대출건수','도서권수']], vert = False)
plt.xscale('log') # 주의! 그림을 수평으로 바꾸면 스케일도 반대로 바뀐다.
plt.show()

3) 수염길이 조정하기
- 기본적으로 수염 길이는 IQR의 1.5배
- 수염 길이 조정 : boxplot()의 whis 매개변수에서 조정 가능 ( 기본값 : 1.5)
- 방법1. IQR 길이에 따른 수염길이 조정
-> whis = 10 -> IQR의 10배로 수염길이 그리
- 방법2. 백분위수로 수염길이 조정
-> whis = (10,90) -> 10%, 90% 백분위수에 해당하는 데이터까지 수염을 그림
# IQR 길이에 따른 수염길이 조정
plt.boxplot(ns_book7[['대출건수','도서권수']], whis = 10)
plt.yscale('log')
plt.show()
# 백분위수로 수염길이 조정
plt.boxplot(ns_book7[['대출건수','도서권수']], whis = (0,100))
plt.yscale('log')
plt.show()
